Підвищення результативності навчання на уроці спостерігається з активним використанням інформаційно-комунікаційних технологій, відповідно впровадження таких засобів у навчальний процес свідчить про розвиток логічного мислення та творчих здібностей школярів. Спостерігаються серед учнів самостійні рішення і виконання необхідних дій, що призводить до розв’язку поставленої задачі, та є реалізацією проблемного підходу у навчанні.
Метою дослідження є використання інформаційно-комунікаційних технологій на уроках природничо-математичного профілю в основній школі.
Задачею школи є підготовка всесторонньо розвиненої, активної особистості, здатної до самостійних досліджень і відкриттів. Така особистість має володіти методами аналізу і синтезу, абстрагування й узагальнення, вмінням доводити і спростовувати, робити правильні висновки, приймати обґрунтовані, раціональні рішення.
Підсилення мотивації навчально-пізнавальної діяльності учнів при навчанні математики можливе завдяки особистості вчителя, правильній постановці цілей навчання, створення сприятливих умов для зацікавленої роботи учнів, формування установок на досягнення успіху [1].
Важливим і поширеним видом розв’язування задач шкільного курсу є математичне моделювання, де дослідження здійснюється з використанням моделі, сформульованої у вигляді математичних виразів.
Під моделлю розуміємо таку розумово-уявну або матеріально реалізовану систему чи фізичний об’єкт, яка відображає та відтворює об’єкт дослідження і здатна замінити його так, що її подальше вивчення та дослідження дає нам нові повідомлення про цей об’єкт. Під моделюванням розуміють процес формалізації фізичного об’єкта, метою якого є створення певного аналогу об’єкта, його моделі, адекватної йому [2].
Математичне моделювання як один з найефективніших методів наукового дослідження, є комплексне дослідження властивостей фізичного об’єкта з допомогою створеної його математичної моделі за допомогою ІКТ, включає в себе наступний ряд етапів [2]: фізична постановка задачі, створення математичної моделі, розробка методу побудови розв’язку моделі, його алгоритмізації та програмної реалізації за допомогою ІКТ, перевірка математичної моделі на адекватність, дослідження на математичній моделі, перенесення одержаних на математичній моделі даних на фізичний об’єкт, вивчення і використання одержаних даних в практичній діяльності.
На прикладі проілюструємо прийоми й методи математичного моделювання. Побудувати математичну модель біологічного процесу розмноження бактерій, отримати дані про еволюцію цього процесу, можливі варіанти цих змін залежно від початкового стану.
Швидкість поділу бактерій пропорційна кількості бактерій N у даний момент часу t. Диференціальне рівняння закону розмноження має такий вигляд:
Try another browser to show content,де k – коефіцієнт розмноження. Інтегральний закон розмноження бактерій описується такою формулою:
Try another browser to show content,
де Try another browser to show content. Якщо k > 0, то бактерії з плином часу зростають, k=0– залишаються незмінними N(t)=N(0)=, k < 0 - зменшуються та з часом гинуть.
Блок-схема закону розмноження бактерій має вигляд (див. рис. 1.)
В ході моделювання динаміки процесу розмноження бактерій отримано результати (див. рис. 2.).
З початковою чисельність Try another browser to show content, та початковим терміном 2004р. результати залежать від коефіцієнту розмноження.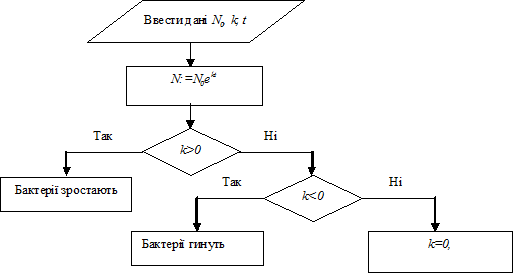
Рис. 1. Блок-схема закону розмноження бактерій
Рис.2. Моделювання динаміки чисельності бактерій
В наш час розроблено та застосовується велика кількість програмних засобів, використання яких дозволяє розв’язувати за допомогою комп’ютера досить широке коло математичних задач різних рівнів складності. Одним з таких програмних засобів є система динамічної математики GeoGebra.
GeoGebra – вільно розповсюджений пакет комп’ютерної математики, що поєднує можливості динамічної геометрії з аналітичними обчисленнями. Використання даного пакету у процесі навчання математики надає можливість створювати динамічні побудови, а також виконувати такі дії:
1) проводити та документувати різні обчислення: числові (точні, наближені з указаною точністю), аналітичні (дії з алгебричними виразами, розв’язування рівнянь, інтегрування, диференціювання);
2) візуалізувати аналітичні залежності (будувати графіки функцій однієї змінної, криві другого порядку та параметрично задані функції), виконувати статистичне опрацювання результатів експерименту, побудову діаграм та гістограм, а також рисунків за допомогою графічних примітивів;
3) зберігати у файлах, роздруковувати та пересилати по мережі файли з обчисленнями чи графікою;
4) створювати якісну анімацію графічних образів.
GeoGebra орієнтована на користувача, який не є професіоналом у галузі програмування, а має тільки базову підготовку [3].
GeoGebra має великий набір інструментів для створення динамічних комп’ютерних моделей. На сучасному етапі розвитку шкільної освіти використання комп’ютерних моделей у навчальному процесі є однією з передумов підвищення його результативності. Комп’ютерні моделі можна використовувати з різною метою, а саме [4]: інтерактивні комп’ютерні моделі як динамічні наочні посібники; інтерактивні комп’ютерні моделі, що використовуються для організації евристичного навчання; моделі, що призначені для автоматизації обчислень; інтерактивні комп’ютерні моделі для автоматизації процесу створення навчальних вправ і завдань.
Методична система навчання з використанням моделювання будується на концепціях теорії проблемного навчання та теорії поетапного формування розумових дій, що забезпечує можливість управління навчальною діяльністю і створення орієнтувальної основи дій для розвитку творчих здібностей. Таке навчання забезпечує формування наукового світогляду.
Список літератури:
1. Психолого-педагогічні вимоги до комп’ютерно-орієнтованих систем навчання математики. / Гриб’юк О.О., Жалдак М.І. // Науковий часопис Національного педагогічного університету імені М.П. Драгоманова. Серія 2: комп’ютерно-орієнтовані системи навчання: Зб. наук. праць – К.: НПУ імені М.П. Драгоманова., 2013. – С. 3 – 19.
2. Гриб’юк О.О. Математичне моделювання як засіб екологічного виховання учнів у процесі навчання математики в класах хіміко-біологічного профілю / О.О. Гриб’юк // Дидактика математики: проблеми і дослідження: Міжнародний збірник наукових робіт. – Вип. 27. – Донецьк.: Фірма ТЕАН, 2007. – С. 132 – 139.
3. Пікалова В. В. GeoGebra. Загальна інформація [Електронний ресурс] / Валентина Валеріївна Пікалова // Кафедра інформатики Харківського національного педагогічного університету імені Г.С. Сковороди – Режим доступу до ресурсу: http://kafinfo.org.ua/geogebra.
4. Ракута В. М. Система динамічної математики GeoGebra як інноваційний засіб для вивчення математики [Електронний ресурс] / В. М. Ракута // Інформаційні технології і засоби навчання. – 2012. – Режим доступу до ресурсу: http://www.journal.iitta.gov.ua
